Cuckoo filter

Reference: Fan, Andersen, Kaminsky & Mitzenmacher: "Cuckoo Filter: Practically Better Than Bloom"

What it is

A cuckoo filter is conceptually similar to a bloom filter, even though the underlying algorithm is quite different.

The cuckoo filter is similar to a Set. Hashable objects can be pushed into the filter, but objects cannot be extracted from the filter. Querying the filter, i.e. asking whether an object is in a filter is fast, but cuckoo filters has a certain probability of falsely returning true when querying about an object not actually in the filter. When querying an object that is in the filter, it is guaranteed to return true.

A cuckoo filter is defined by two parameters, F and its length L. Memory usage is F*L/2 bytes plus 50-ish bytes of overhead, and the false positive rate is approximately 9*(N/L)*(2^-F) where N is the number of elements in the filter.

Querying (in)

Querying takes one cache access plus either 1 or 2 random memory access depending on the values of N, F and L, and so can be thought of as being constant. When querying about an object in the filter, it is guaranteed to return true, unless deletion operations have been done on the filrter. Querying about objects not in the filter returns true with a probability approximately to 9*(N/L)*(2^-F).

In general, two distinct objects A and B will have a 1/(2^F-1) chance of sharing so-called "fingerprints". Independently, each object is assigned two "buckets" in the range 1:L/4, and inserted in an arbitrary of the two buckets. If objects A and B share fingerprints, and object A is in one of B's buckets, the existence of A will make a query for B return true, even when it's not in the filter.

Pushing (push!)

Only hashable objects can be inserted into the filter. Inserting time is stochastic, but its expected duration is proportional to 1/(1 - N/L). To avoid infinite insertion times as N approaches L, an insert operation may fail if the filter is too full. A failed push operation returns false.

Pushing may yield false positives: If an object A exists in the filter, and querying for object B would falsely return true, then pushing B to the filter has a probability 1/2 + 1/2 * N/L of returning true while doing nothing, because B is falsely believed to already be in the filter.

Deletion (pop!)

Objects can be deleted from the filter. Deleting operation also exhibits false positives: If B has been pushed to the filter, falsely returning success, then deleting A will also delete B.

Deletion of objects is fast and constant time, except if the filter is at full capacity. In that case, it will attempt to self-organize after a deletion to allow new objects to be pushed. This might take up to 200 microseconds.

FastCuckoo and SmallCuckoo

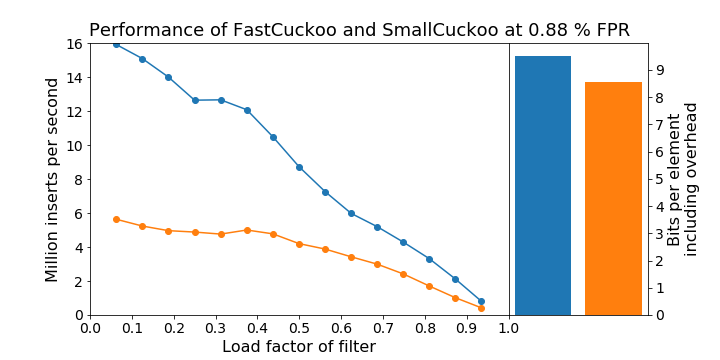
Probably.jl comes with two different implementations of the cuckoo filter: FastCuckoo and SmallCuckoo. The latter uses a more complicated encoding scheme to achieve a slightly smaller memory footprint, but which also make all operations slower. The following plot shows how the speed of pushing objects depend on the load factor, i.e. how full the filter is, and how FastCuckoos are ~2.5x faster than SmallCuckoos, but that the SmallCuckoo uses about 10% less memory. FastCuckoo is displayed in blue, SmallCuckoo in orange.

Usage example

For this example, let's say I have a stream of kmers that I want to count. Of course I use BioJulia, so these kmers are represented by a DNAKmer{31} object. I suspect my stream has up to 2 billion different kmers, so keeping a counting Dict would use up all my memory. However, most kmers are measurement errors that only appear once and that I do not need spend memory on keeping count of. So I keep track of which kmers I've seen using a Cuckoo filter. If I see a kmer more than once, I add it to the Dict.

params = constrain(SmallCuckoo, fpr=0.02, capacity=2_000_000_000)
if params.memory > 4e9 # I'm only comfortable using 4 GB of memory for this
    error("Too little memory :(")
end
filter = SmallCuckoo{params.F}(params.nfingerprints)
counts = Dict{Kmer, UInt8}() # Don't need to count higher than 255

for kmer in each(DNAKmer{31}, fastq_parser)
    if kmer in filter
        # Only add kmers we've seen before
        count = min(0xfe, get(counts, kmer, 0x01)) # No integer overflow
        counts[kmer] = count + 0x01
    else
        push!(filter, kmer)
    end
end

Interface

Construction

A cuckoo filter can be constructed directly from the two parameters F and L, where L is the number of fingerprint slots in the fingerprint. Remember that L should be a power-of-two:

julia> FastCuckoo{12}(2^32) # F=12, L=2^32, about 6 GiB in size

However, typically, one wants to construct cuckoo filters under some kind of constrains: Perhaps I need to store at least 1.1 billion distinct elements, with a maximal false positive rate of 0.004. For this purpose, use the constrain function.

This function takes a type and two of three keyword arguments:

• fpr: Maximal false positive rate
• memory: Maximal memory usage
• capacity: Minimum number of distinct elements it can contain

It returns a NamedTuple with the parameters for an object of the specified type which fits the criteria:

julia> constrain(SmallCuckoo, fpr=0.004, capacity=1.1e9)
(F = 11, nfingerprints = 2147483648, fpr = 0.002196371220581028, memory = 2952790074, capacity = 2040109466)

Having passed false positive rate and capacity, the function determined the smallest possible SmallCuckoo that fits these criteria. We can see from the fields F and nfingerprints that such a SmallCuckoo can be constructed with:

SmallCuckoo{11}(2147483648)

Furthermore, we can also see that those particular constrains were quite unlucky: The actual false positive rate of this filter will be ~0.0022 (at full capacity), and its actual capacity will be ~2 billion elements. It is not possible to create a smaller SmallCuckoo which fits the given criteria.

Central functions

in(item, filter::AbstractCuckooFilter)

push!(filter::AbstractCuckooFilter, items...)

pop!(filter::AbstractCuckooFilter, item)

julia> a = FastCuckoo{12}(2^4); push!(a, 1); push!(a, 868)
julia> pop!(a, 1); # Remove 1, this accidentally deletes 868 also
julia> isempty(a)
true

Misc functions

Base.copy!
Base.copy
Base.sizeof # This one includes the underlying array

isempty(x::AbstractCuckooFilter)

julia> a = FastCuckoo{12}(1<<12); isempty(a)
true

empty!(x::AbstractCuckooFilter)

julia> a = FastCuckoo{12}(1<<12); push!(a, "Hello"); isempty(a)
false

julia> empty!(a); isempty(a)
true

union!(dest::HyperLogLog{P}, src::HyperLogLog{P})

julia> # length(c) ≥ length(b) is not guaranteed, but overwhelmingly likely
julia> c = union!(a, b); c === a && length(c) ≥ length(b)
true

union!(dst::AbstractCuckooFilter{F}, src::AbstractCuckooFilter{F})

union(x::HyperLogLog{P}, y::HyperLogLog{P})

julia> # That c is longer than a or b is not guaranteed, but overwhelmingly likely
julia> c = union(a, b); length(c) ≥ length(a) && length(c) ≥ length(b)
true

union(x::AbstractCuckooFilter{F}, y::AbstractCuckooFilter{F})

loadfactor(x::AbstractCuckooFilter)

julia> a = FastCuckoo{12}(1<<12);
julia> for i in 1:1<<11 push!(i, a) end; loadfactor(a)
0.5

fprof(::Type{AbstractCuckooFilter{F}}) where {F}
fprof(x::AbstractCuckooFilter)

fprof(sketch::CountMinSketch)

capacityof(filter::AbstractCuckooFilter)

constrain(T<:AbstractCuckooFilter; fpr=nothing, mem=nothing, capacity=nothing)

julia> # FastCuckoo with FPR ≤ 0.001, and memory usage ≤ 250_000_000 bytes

julia> c = constrain(FastCuckoo, fpr=0.001, memory=250_000_000)
(F = 14, nfingerprints = 134217728, fpr = 0.0005492605216655955, memory = 234881081,
capacity = 127506842)

julia> x = FastCuckoo{c.F}(c.nfingerprints); # capacity optimized

julia> fprof(x), sizeof(x), capacityof(x) # not always exactly the estimate
(0.0005492605216655955, 234881081, 127506842)